자료구조와 알고리즘 - 3 link
14강. 큐(Queues)

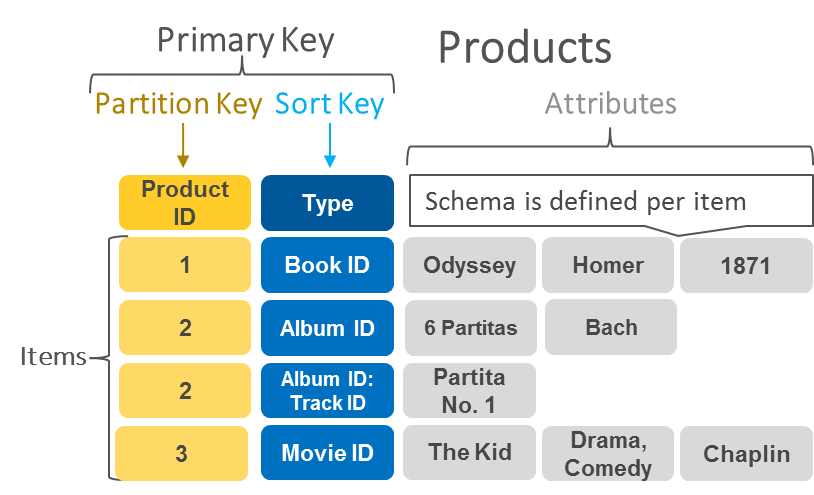
큐는 Stack과 달리 선입선출(FIFO; First-In First-Out) 의 순서로 제어됩니다. 리스트 속에 데이터들의 시작과 끝의 포인터가 존재합니다. 입력(enqueue)시, 리스트의 rear pointer에 추가되며 출력(dequeue)시, 리스트의 front pointer 부분을 꺼내게 됩니다.
실습
목표: 배열과 양방향 연결 리스트 구현시, 연산 복잡도 확인
배열 - 출력시, 모든 개체의 위치를 옮기는 과정에서 O(n) 가 소요
양뱡향 연결 리스트 - 포인터만 변경하게 됨으로 O(1) 소요
15강. 환형 큐(Circular Queue)

dequeue 과정에서 발생한 front pointer 앞의 공간을 재사용하지 못하는 큐의 단점을 개선하여 리스트의 시작과 끝을 이음으로써 재사용 가능
실습
목표: 환형큐의 enqueue, dequeue, peek 구조를 구현
범위가 제한된 배열을 환형으로 이어서 쓴다는점을 감안하여 배열의 끝과 처음을 연속적으로 사용
16강. 우선순위 큐(Priority Queues)
FIFO 의 특성을 가진 일반적인 큐와 달리 우선순위에 따라 enqueue나 , dequeue의 대상이 선택되는 방식.
실습
목표: 양방향 리스트를 통해 enqueue할 때, 순차검색을 통해 일치하는 위치에 넣는 방식 사용, data의 값이 클수록 높은 우선순위.
enqueue => O(n), dequeue = O(1)
트리구조 사용시 더 유용하나 다음 과정에 진행, 퀵정렬과 비슷한 느낌일것으로 예상
17강. 트리(Trees)

트리의 각 노드를 정해진 순서로 방문하는 것, 순회 (traversal) 연산.
- 깊이 우선 순회 (DFT; Depth First Traversal)
- 넓이 우선 순회 (BFT; Breadth First Traversal)
DFT (Depth First Traversal) vs DFS (Depth First Search)? link
- DFT는 DFS를 사용합니다.
- DFS가 연결된 그래프에 적용되는 알고리즘 인 반면, DFT는 일반적으로 연결이 끊어진 그래프에 적용되는 순회입니다.
- DFS는 DFT가 수행하는 동안 각각의 모든 노드를 방문 할 것이라고 보증하지 않았습니다.
하지만 같은것이라 보아도 크게 문제되지 않습니다. 두 용어 모두, 그래프 또는 트리 (모든 트리는 또한 그래프이기도 합니다) 를 대상으로 노드들을 방문하는 순서를 규정하는 방식을 뜻합니다.
근데 tree보단 root모양인데 왜 그렇게 굳어진걸까?
18강. 이진 트리(Binary Trees)
모든 노드의 자식노드; 차수가 2 이하인 트리구조
깊이 우선 순회(DFT; Depth First Traversal)
- 중위 순회 (in-order traverasl): 왼쪽 서브트리를 순회한 뒤 노드 x 를 방문, 그리고 나서 오른쪽 서브트리를 순회
- 전위 순회 (pre-order traversal): 노드 x 를 방문한 후에 왼쪽 서브트리를 순회, 마지막으로 오른쪽 서브트리를 순회
- 후위 순회 (post-order traversal): 왼쪽 서브트리를 순회, 오른쪽 서브트리를 순회, 그리고 나서 마지막으로 노드 x 를 방문
실습 1
목표: 이진트리의 depth 값 계산하는 기능 구현
class Node:
def depth(self):
l = self.left.depth() if self.left else 0
r = self.right.depth() if self.right else 0
return (l if l > r else r) + 1
class BinaryTree:
def depth(self):
if self.root:
return self.root.depth()
else:
return 0
실습 2, 3 - 깊이 우선 순회(DFT; Depth First Traversal)
목표: 이진트리의 전위순회, 후위순회 연산 기능 구현
class Node:
def preorder(self):
traversal = []
traversal.append(self.data)
if self.left:
traversal += self.left.preorder()
if self.right:
traversal += self.right.preorder()
return traversal
def postorder(self):
traversal = []
if self.left:
traversal += self.left.postorder()
if self.right:
traversal += self.right.postorder()
traversal.append(self.data)
return traversal
class BinaryTree:
def preorder(self):
if self.root:
return self.root.preorder()
else:
return []
def postorder(self):
if self.root:
return self.root.postorder()
else:
return []
19강 이진 트리 - 넓이 우선 순회(BFT; Breadth First Traversal)
BFT는 트리 구조에서 낮은 level 중 왼쪽 노드부터 순회하게 됩니다. 이로써 DFT와 달리 재귀적으로 구현이 불가합니다. 하지만 Queue를 사용하여 다음에 방문할 노드를 enqueue 해두고 dequeue 하게되면 각각의 level별로 노드를 순회하게 됩니다.
실습
목표: 넓이 우선 순회 기능을 구현
def bft(self):
traversal = []
queue = ArrayQueue()
if self.root:
queue.enqueue(self.root)
while not queue.isEmpty():
node = queue.dequeue()
traversal.append(node.data)
if node.left:
queue.enqueue(node.left)
if node.right:
queue.enqueue(node.right)
return traversal
20강. 이진 탐색 트리(Bianry Search Trees) (1)

시간복잡도
- Search Operation - O(n)
- Insertion Operation - O(1)
- Deletion Operation - O(n)
퀵정렬의 알고리즘을 트리의 형태로 접근하는 방식으로 생각하면 될 것 같다.
실습
목표: BST 에 insert 기능을 구현
def insert(self, key, data):
if self.key is key:
raise KeyError('inserted key is duplicated')
if self.key > key:
if self.left:
self.left.insert(key, data)
else:
self.left = Node(key, data)
elif self.key < key:
if self.right:
self.right.insert(key, data)
else:
self.right = Node(key, data)
return True
21강. 이진 탐색 트리(Binary Search Trees) (2)
트리노드 삭제시 고려사항 참조
- 하위노드 X

- 1개의 하위노드

- 2개의 하위노드

3번을 처리하며 1, 2의 과정 모두 처리가능
def remove(self, key):
node, parent = self.lookup(key)
if node:
nChildren = node.countChildren()
if nChildren is 0:
if parent:
if node.key is parent.left.key:
parent.left = None
else:
parent.right = None
else:
self.root = None
elif nChildren is 1:
childNode = None
if node.left:
childNode = node.left
else:
childNode = node.right
if parent:
if node.key is parent.left.key:
parent.left = childNode
else:
parent.right = childNode
else:
self.root = childNode
else:
parent = node
successor = node.right
while successor.left:
parent = successor
successor = successor.left
node.key = successor.key
node.data = successor.data
if successor.key is parent.left.key:
parent.left = successor.right
else:
parent.right = successor.right
return True
else:
return False
22강. 힙(Heaps)
힙 (heap) 도 이진 트리의 한 종류이며 이진 힙 (binary heap) 이라고도 불립니다.
힙에는 최대 힙 (max heap) 과 최소 힙 (min heap) 이 있습니다. 최대 힙과 최소 힙은 데이터 원소의 순서 기준이 내림차순이냐 오름차순이냐만 달라지고 완전히 대칭이므로, 여기에서는 최대 힙을 기준으로 설명을 전개하겠습니다. 최대 힙은 세 가지의 성질을 유지하고 있는 이진 트리입니다. 그 세 가지 성질은:
- 루트 노드가 항상 최댓값을 가진다.
- 완전 이진 트리이다. (최하위 레벨을 제외하고 모든 레벨이 차있는 상태)
- 최대 힙 내의 임의의 노드를 루트로 하는 서브트리 또한 최대 힙이다.
완전이진트리의 제약조건으로 인해 log(n)에 비례하는 실행시간을 가짐
배열을 이용해 이진트리 표현시 index 는
*노드 번호 n 기준
- 상위 : m // 2
- 좌측 하위: 2 * n
- 우측 하위: 2 * n + 1
실습
목표: 새로운 노드 추가
def insert(self, item):
self.data.append(item)
index = len(self.data)-1
while index > 1:
if(self.data[index] > self.data[index // 2]):
self.data[index] = self.data[index // 2]
self.data[index // 2] = item
index = index // 2
else:
break
23강. 힙(Heaps) (2)
최대 힙에서의 삭제. logn의 복잡도
- 루트노드의 제거 (루트노드에 최대값이 위치)
- 트리의 마지막 노드를 루트노드로 이동
- 양쪽 자식노드보다 작을때 까지 서로 값을 교환 (자식노드 중 둘다 클경우 더 큰쪽으로)
최대/최소 힙의 응용
우선 순위 큐 (priority queue)
삽입(enqueue)시, 느슨한 정렬(=반정렬; 큰값이 상위, 작은값이 하위에 있음)을 이루고 있도록 함. O(logn) 의 복잡도
출력(dequeue)시, 최대값을 순서대로 추출. O(logn) 의 복잡도
힙 정렬 (heap sort)
정렬되지 않은 원소를 최대힙에 삽입, O(logn) X 힙이 빌때까지 삭제순으로 정렬, O(logn) = O(nlogn)